搜索

深度优先搜索

深度优先搜索即 “Depth First Search”，简称DFS。在寻找目标问题的解时，以深度优先，按照相同步骤一直找下去，直到找到解或确定无法找到解，则返回上一步骤，继续按同样的方法寻找解。深度优先搜索的思想基于递归算法，解决递归算法的问题可将问题划分为两步：一.确定边界条件；二.划分子问题。

例:以下图的二叉树为例，深度优先搜索的对树的访问顺序是A->B->D->G->H->C->E->J->F

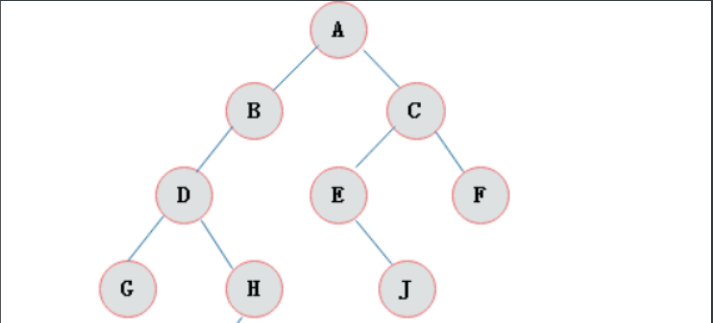
image-20210405172952505

创建该树:

//该树的结点结构体
struct TreeNode {
	char ch;
	TreeNode* left, * right;
	TreeNode() :left(nullptr), right(nullptr),ch('#') {
	}
};
//没有叶子节点的位置用'#'代替叶子节点
char tree[] = { 'A','B','C','D','#','E','F','G','H','#','#','#','J','#','#' };
//递归创建树
void createTree(TreeNode* &node, int ch) {
	if (tree[ch] == '#' || ch > 14) {
		return;
	}
	node = new TreeNode;
	node->ch = tree[ch];
	createTree(node->left, ch * 2 + 1);
	createTree(node->right, ch * 2 + 2);
}

//访问函数，访问可以是任意操作，不一定是输出
void visit(TreeNode* p) {
	cout << p->ch << " ";
}

DFS算法实现:

//深度优先搜索
void dfs(TreeNode* node) {
	visit(node);//访问节点
    //子问题:每个节点都有左右节点，子问题就是搜索左节点，搜索右节点。
	if(node->left)
		dfs(node->left);
	if(node->right)
		dfs(node->right);
    //边界条件:搜索结束条件是左右节点都是空节点，空节点不妨问，直接返回。
}

例题:

全排列问题

#include <iostream>
#include <stdio.h>
using namespace std;

int n;
bool visit[10] = {false};
int result[10] = {0};

void dfs(int step){
	//边界条件:当将要取数个数大于了n个，表示已经取数已经完成，可以直接输出
	if(n + 1 == step){
		for(int i = 1;i <= n;i++){
			printf("%5d",result[i]);
		}
		printf("\n");
		return;	 
	}
	//确定子问题:要确定一个排列，只需在n步中，每步取走一个数，剩余的数交给后面的步来完成
	for(int i = 1;i <= n;i++){
		if(!visit[i]){
			visit[i] = true;
			result[step] = i;
			dfs(step+1);
			visit[i] = false;
		}
	}
}
int main(){
	cin >> n;
	dfs(1);
	return 0;
}

广度优先搜索

广度优先搜索即 “Breadth First Search”,简称BFS。在寻找目标问题的解时，以广度优先。

以下图图的遍历为例，DFS算法访问完A后，是先对B及B的子节点进行遍历，再对C及C的子节点遍历，即树的先序遍历。而BFS算法是访问完A后，对B、C节点先进行遍历，再对其子节点进行遍历，即先访问第一层，再访问第二层，再访问第三层……即树的层次遍历。对树的访问顺序是A->B->C->D->E->F->G->H->J

image-20210405172952505

BFS算法实现:

void bfs(TreeNode* node) {
	queue<TreeNode*> q;
	q.push(node);
    TreeNode* p = nullptr；
	while (!q.empty()) {
		p = q.front();
		q.pop();
		visit(p); //每次从队列中取出要访问的节点进行访问
        
        //将节点的可访问子节点加入访问队列
		if (p->left)  q.push(p->left);
		if (p->right) q.push(p->right);
	}
}

例：给定一个矩阵，求从矩阵左上角到右下角的需要走的最短的步数(起点也算一步)。说明:每次只能走一步，只能上下左右方向走，不能斜着走，红色格子表示墙，不能走，蓝色格子表示起点和终点，白色格子表示可以走的路径。(矩阵中红色格子用0表示，蓝色和白色用1表示)

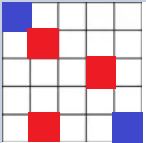
image-20210405220452982

第一行输入N,M,表示矩阵的行和列

第2~N+1行，输入矩阵对应的值

数字之间用空格隔开，1 <= n,m<=10;

对于上图所示应

输入：

5 5

1 1 1 1 1

1 0 1 1 1

1 1 1 0 1

1 1 1 1 1

1 0 1 1 1

输出：

9

#include <iostream>
#include <queue>
using namespace std;
int n, m;
int maze[11][11];
//判断下一个点是否可行
bool visit(int x, int y) {
	if (1 <= x && x <= m && 1 <= y && y <= n && maze[y][x] == 1) {
		return true;
	}
	return false;
}
//广度优先搜索
int bfs() {
	pair<int, int> start(1, 1);
	queue<pair<int,int>> q;
	q.push(start);
	while (!q.empty()) {
		pair<int, int> p = q.front();
		q.pop();
		if (visit(p.first + 1, p.second)) {
			pair<int, int> temp(p.first + 1, p.second);
			maze[temp.second][temp.first] += maze[p.second][p.first];
			q.push(temp);
		}
		if (visit(p.first, p.second+1)) {
			pair<int, int> temp(p.first, p.second+1);
			maze[temp.second][temp.first] += maze[p.second][p.first];
			q.push(temp);
		}
	}
	return maze[n][m];
}
int main() {
	cin >> n >> m;
	for (int i = 1;i <= n;i++) {
		for (int j = 1;j <= m;j++) {
			cin >> maze[i][j];
		}
	}

	cout << bfs();

	return 0;
}

搜索技巧

记忆化搜索

记忆话搜索，即 “Memory Search”，简称MS：记忆化搜索实际上是DFS的优化版。对于已求出的结果，将其保存起来，当之后的搜索结果需要用到之前的搜索结果时，可直接取出，避免重复搜索，从而实现DFS的优化。

例:求斐波那契数列：1，1，2，3，5……中第20个数字。

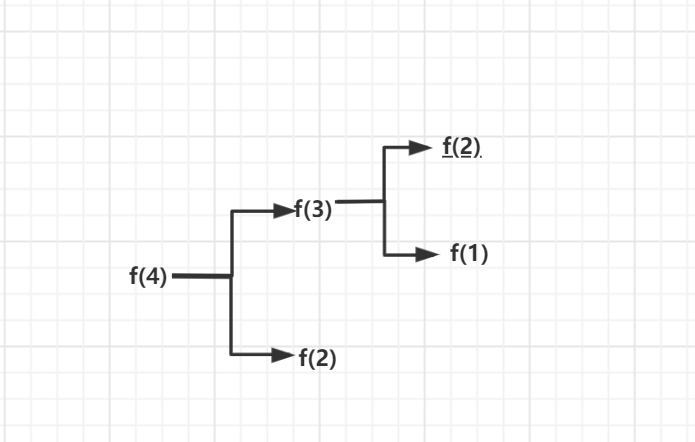
image-20210405231835821

DFS算法求解该题:

int dfs(int n){
    if(n == 1 || n == 2){
        return 1;
    }
    return dfs(n - 1) + dfs(n - 2);
}

可以看出，用DFS求解该题时，在上图的dfs(2)会被重复计算，同理，当n更大时，被重复计算的数会更多。时间复杂度

O(2^n)

int map[100] = { 0 };
map[1] = 1;
map[2] = 1;
int ms(int n) {
       if (map[n]) {
        return map[n];
    }
    map[n] = ms(n - 1) + ms(n - 2);
    return map[n];
}

将每次计算的结果存放后，后面用到前面计算的结果时,直接根据索引查找到对应的值，不需要再递归计算。时间复杂度变为了O(n)

路径回溯

回溯法：又称试探法，选择路径进行探索，如果可行，到达该路径并继续探索，直到找到可行路径或找不路径，返回上一路径，重新探索新路径，回溯的思想可以理解为：不撞南墙不回头。

例:

八皇后问题

回溯算法求解:

#include <iostream>
using namespace std; 
char maze[8][8]={0};
int n = 0;
//判断（x,y）坐标是否可以摆放皇后 
bool can_down(int x,int y){
    //检查左方是否有棋子
	for(int i = x;i >= 0;i--){
		if(maze[y][i] == '0'){
			return false;
		}
	}
	//检查左上方是否有棋子
	for(int i = x,j = y;i >= 0 && j >= 0;i--,j--){
		if(maze[j][i] == '0'){
			return false;
		}
	}
	//检查左下方是否有棋子
	for(int i = x,j = y;i >= 0 && j < 8;i--,j++){
		if(maze[j][i] == '0'){
			return false;
		}
	}
	return true;
}

//打印棋盘 
void print_checkerboard(){
	for(int i = 0;i < 8;i++){
		for(int j = 0;j < 8;j++){
			cout << maze[i][j];
		}
		cout << endl;
	}
	n++;
	cout <<n<< endl;
}
//从左往右每列下一颗棋子
void eight_queens(int x){
	if(x == 8){
		print_checkerboard();
	}
	
	for(int j = 0;j < 8;j++){
		if(can_down(x,j)){
			maze[j][x] = '0';
			eight_queens(x+1);
			maze[j][x] = '#';//每次找到或未找到都需将该位置的状态重置
		}
	}
}
//初始化棋盘 
void init_checkerboard(){
	for(int i = 0;i < 8;i++){
		for(int j = 0;j < 8;j++){
			maze[i][j] = '#';
		}
	}
}

int main(){
	init_checkerboard();
	eight_queens(0);
}

剪枝

剪枝:对于目标问题，我们可以预先知道正确解的规律，因此在搜索前或搜索过程中直接停止对明显不符合题意的解进行搜索，这个操作就成为剪枝，可大大提高搜索效率。

常见的剪枝有以下几种:

1.可行性剪枝

当当前状态和题意明显不符时直接返回，停止继续搜索

2.排除等效冗余

当多个分支相同时不必对每个分支进行相同的搜索，只选择其中一个就可以了

3.最优性剪枝

对于求最优解问题，正在搜索的解的状态已经比已经搜得的最优解不优时，可以认定正在搜索的解不是最优解，直接剪掉

4.顺序剪枝

……

5.记忆化

就是记忆化搜索

例:求10000以内全部素数。

#include <iostream>
using namespace std;
int prime[10000];
int main() {
	prime[0] = 2;
	prime[1] = 3;
	prime[2] = 5;
	
	int n = 7;
	int count = 2;
	while (count < 10000) {
		int flag = 1;
		for (int i = 0;i <= count;i++) {
			if (n % prime[i] == 0) {//如果不是素数，那么它应该能被素数整除（可行性剪枝）
				flag = 0;
			}
		}
		if (flag) {
			count++;
			prime[count] = n;//将搜索到的素数存放到素数数组中,记忆化搜索
		}
		n % 6 == 5 ? n += 2 : n += 4;//除了2，3，所有的素数都不能被2和3整除，那么所有的素数都在6的倍数附近，如5，7  11,13  17，19 ……，所以素数应该在6n-1或6n+1中去找，将n++改为n % 6 == 5 ? n += 2 : n += 4;可以直接剪掉不能成为素数的数(顺序剪枝)
	}
	for (int i = 0;i < 10000;i++) {
		cout << prime[i] << endl;
	}

	return 0;
}